Abstract

Discovery and learning of an underlying spatiotemporal hierarchy in sequential data is an important topic for machine learning. Despite this, little work has been done to explore hierarchical generative models that can flexibly adapt their layerwise representations in response to datasets with different temporal dynamics. Here, we present Variational Predictive Routing (VPR) – a neural probabilistic inference system that organizes latent representations of video features in a temporal hierarchy, based on their rates of change, thus modeling continuous data as a hierarchical renewal process. By employing an event detection mechanism that relies solely on the system’s latent representations (without the need of a separate model), VPR is able to dynamically adjust its internal state following changes in the observed features, promoting an optimal organisation of representations across the levels of the model’s latent hierarchy.

Architecture

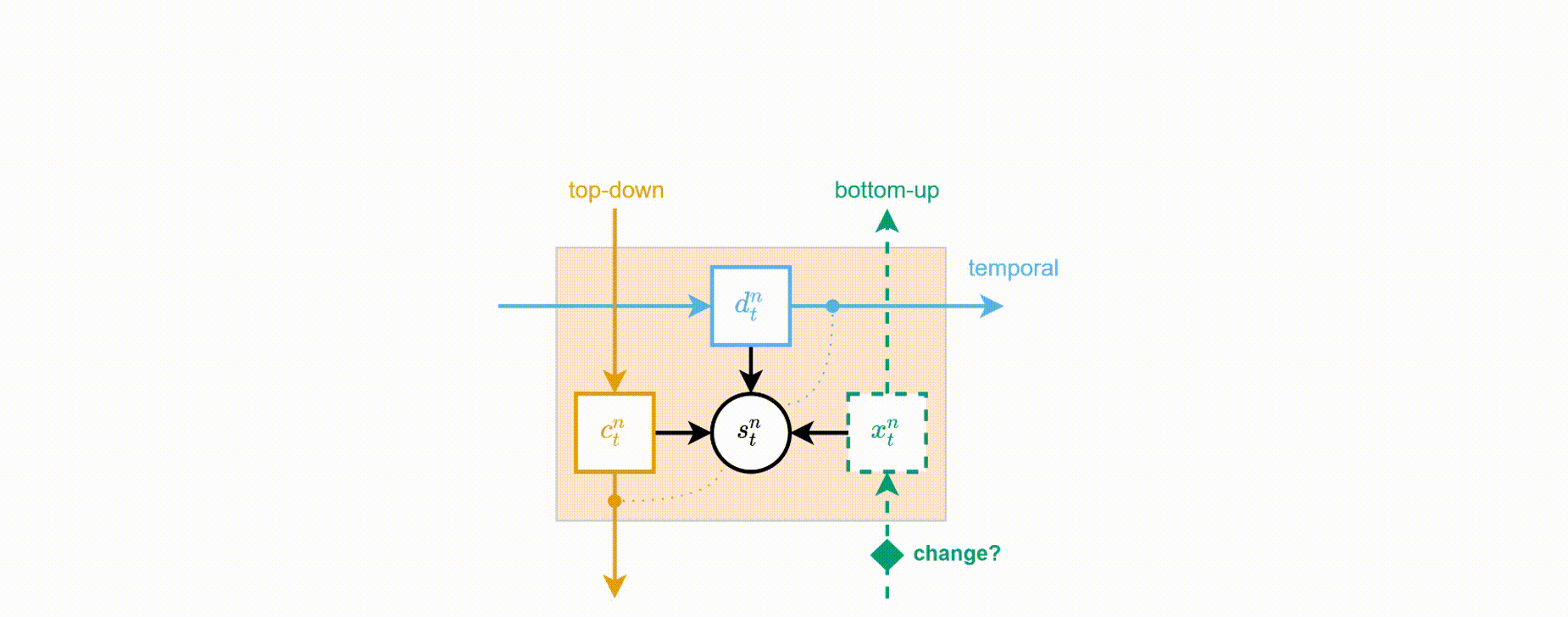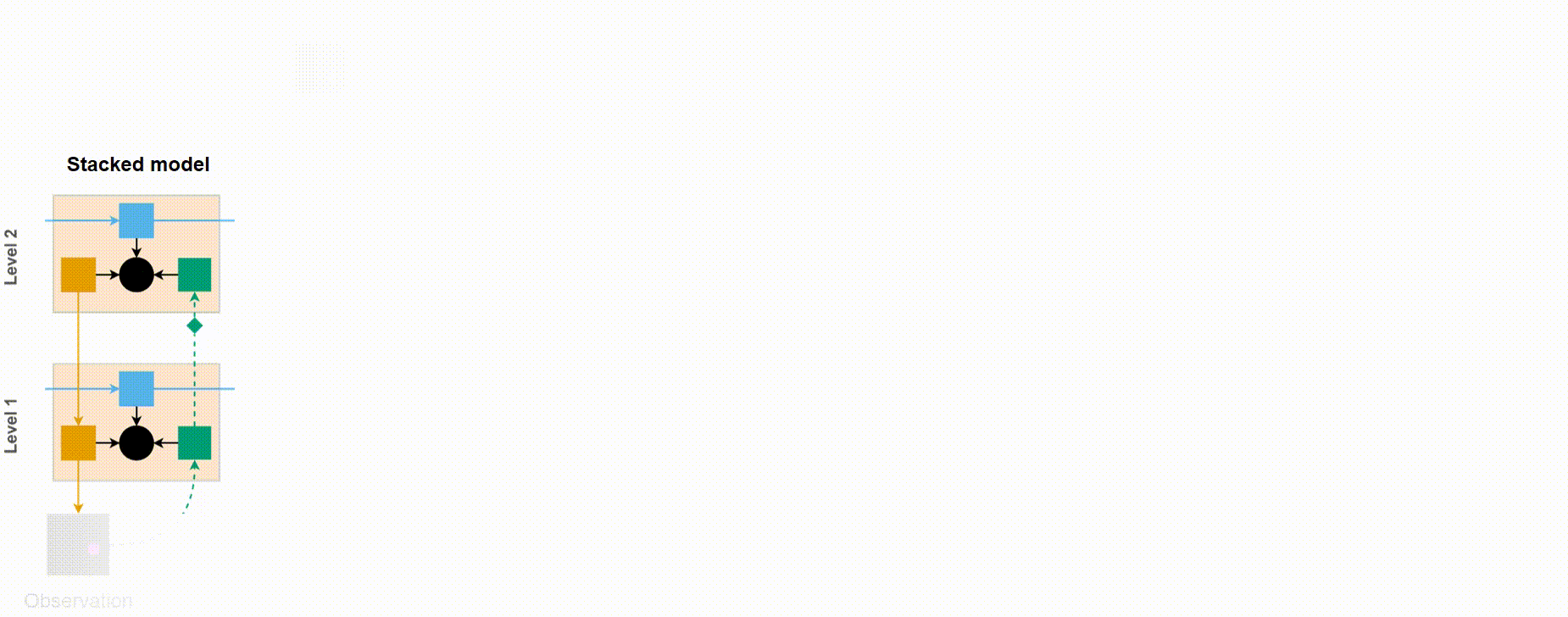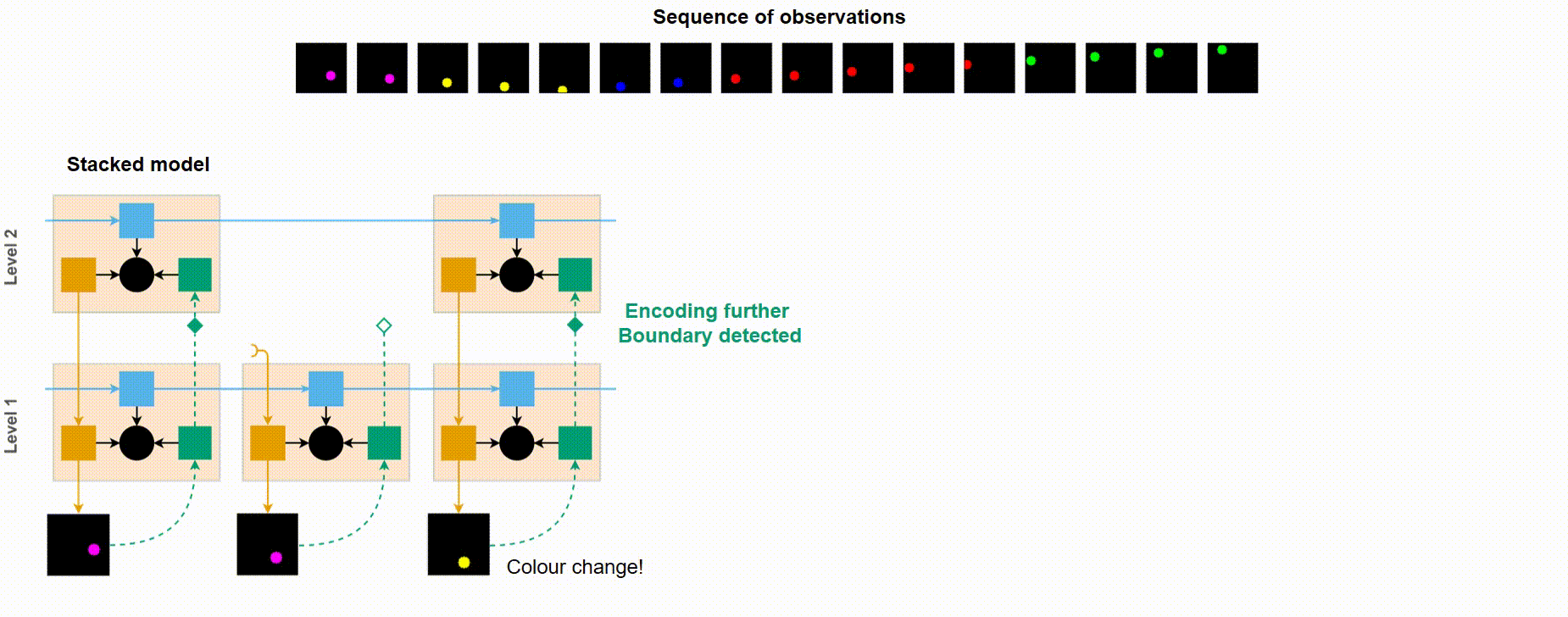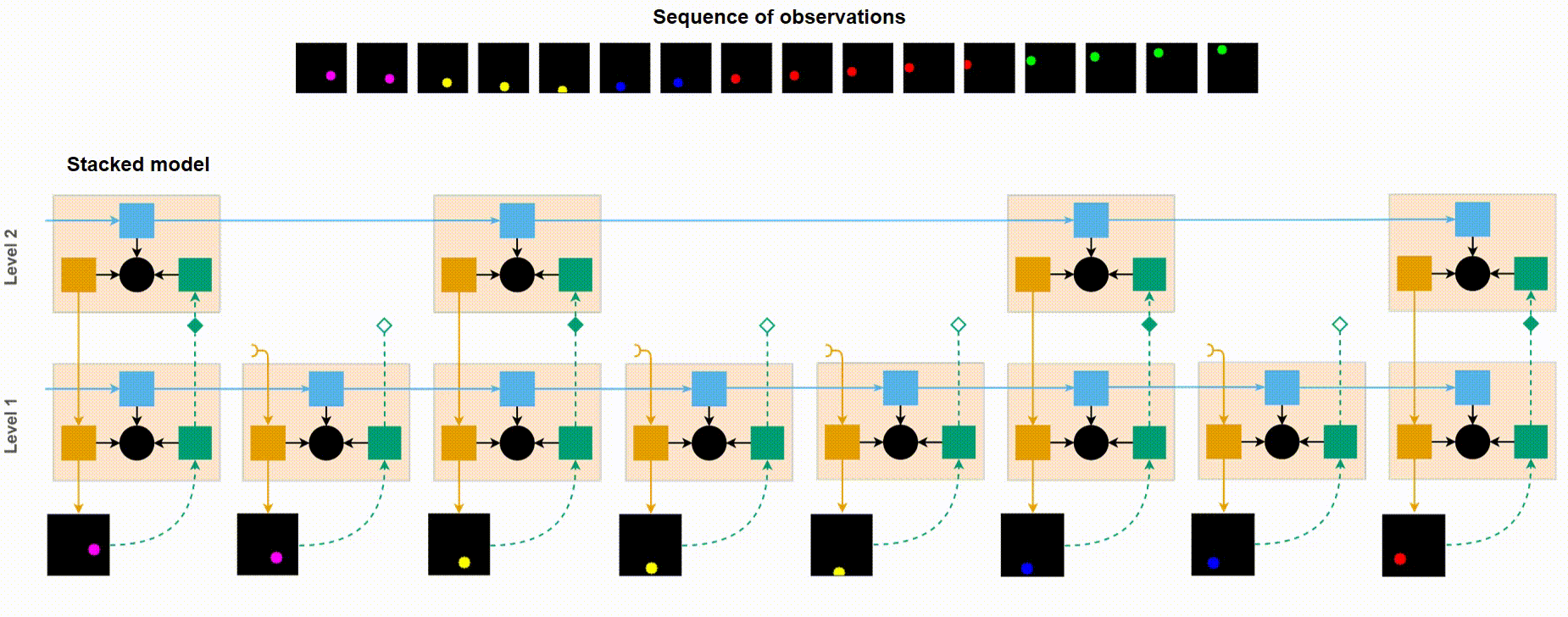
Building blocks of VPR

VPR consists of computational blocks that are stacked together in a hierarchy. Figure on the right shows the insides of a single block with key variables and channels of information flow. Each block in layer \(n\) consists of three deterministic variables \((x^n_t, c^n_t, d^n_t)\) that represent the three channels of communication between the blocks: bottom-up (encoding), top-down (decoding), and temporal (transitioning), respectively. These variables are used to parametrise a random variable \(s^n_t\) that contains the learned representations in a given level of the hierarchy. Figure below shows an example of a three-level VPR model unrolled over five timesteps, demonstrating how communications between the blocks are realised over time.

Example of a three-level VPR model unrolled over five timesteps.

Event boundary detection: enforcing temporal hierarchy

You may have noticed that the unrolled model updates its states at different times and with different rates - how does the model decide on that?

At the heart of VPR is a mechanism that is used for detecting predictable and unpredictable changes in the observable features over time, and thus determine the boundaries of events. At every level of the model, the event detection is used for controlling the structure of the unrolled model over time by allowing or disallowing propagation of bottom-up information to the higher levels of the hierarchy.

Event detection system serves two primary functions in our model:

1. Detecting layerwise events in a sequence of observations is utilised for triggering an update on a block’s state by inferring its new posterior state. Matching block updates with detectable changes in layerwise features (event boundaries) prompts VPR to represent spatiotemporal features in levels that most closely mimic their rate of change over time. Similarly, learning to transition between states only when they signify a change in the features of the data means that VPR learns to make time-agnostic (or jumpy) transitions – from one event boundary to another.
2. Second, the detection mechanism is used for blocking bottom-up communication and thus stopping the propagation of new information to the deeper levels of the hierarchy. This is meant to encourage the model to better organise its spatiotemporal representations by enforcing a temporal hierarchy onto its generative process.

Short demonstration of how VPR works using the Moving Ball dataset. Notice how bottom-up signal propagates up only when the ball’s colour changes (i.e. an event boundary has been detected).

Experiments and results

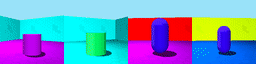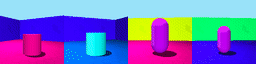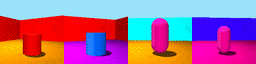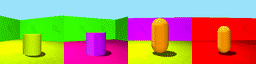
Datasets: 3DSD and Moving Ball. 3D Shapes Dynamic (3DSD) includes three colour features that change with different periodicity. Moving Ball includes a moving ball that changes colour upon a wall bounce or at a random time.

• VPR accurately detects event boundaries. VPR’s event detection mechanism quickly achieves high F1 score in the Moving ball (F1 = \(0.97\pm0.03\)), and 3DSD (F1 = \(0.97\pm0.02\)) datasets. We also observe a significantly better performance compared to the existing temporal abstraction model VTA (Kim, 2019), which achieves a maximum of \(0.52\pm0.05\) F1 score in the Moving Ball dataset.

• VPR learns hierarchical and temporally-disentangled representations. VPR employs its hierarchical structure to disentangle the temporal features extracted from the dataset. Each layer of VPR is equipped with an event detection mechanism that guides the model to distribute representations of temporal features across the hierarchy and learn jumpy predictions between event boundaries.

• VPR can adapt to datasets with different temporal dynamics. To test this property, we instantiate two versions of the Moving Ball dataset – with fast and slow ball movements. In our experiments, we show that VPR performs about 30% fewer block updates under slow ball movement compared to VPR under fast ball movement, while maintaining high F1 score of event detection in both cases.

• VPR produces accurate time-agnostic rollouts of the future. VPR was tested using jumpy layerwise rollouts of length 200 for the Moving Ball and 3DSD datasets, which were evaluated against the ground-truth event sequences. Its performance of future event prediction was compared to a powerful video prediction model, CW-VAE (Saxena, 2021), which produces rollouts over the physical timescale and thus requires longer rollouts to reach an equivalent of VPR’s jumpy predictions. For instance, predicting 200 events of object colour changes in the 3DSD corresponds to a physical rollout of 1600 steps.

Layerwise rollouts using VPR. GT denotes ground-truth sequence, L1 rollouts made using level 1, and so on. To produce layerwise rollouts, the model predicts the next state \(s^n_{\tau+1}\) in the relevant level \(n\) and decodes under fixed states in all other levels. The produced rollouts illustrate model’s ability to learn disentangled representations and produce accurate and feature-specific jumpy rollouts. For Moving Ball, VPR learns to represent the ball’s position and colour in the two separate levels (L1 and L2, respectively). Similar behaviour can be observed using a three-level VPR and the 3D Shapes dataset. VPR learns to represent the three temporal factors of variation across the three levels of its latent hierarchy and to produce jumpy rollouts that correctly predict the changes in the corresponding features.

Random samples taken from the different levels of VPR. The model is able to generate diverse images with respect to the spatiotemporal features represented in the sampled level, while keeping all other features fixed.

Cite us!

@inproceedings{VPR2022,
  title={Variational Predictive Routing with Nested Subjective Timescales},
  author={Alexey Zakharov and Qinghai Guo and Zafeirios Fountas},
  booktitle={International Conference on Learning Representations},
  year={2022},
  url={https://openreview.net/forum?id=JxFgJbZ-wft}
}